|
|
2.1:程序=算法+数据结构
一个程序主要包括以下两方面的信息:
在程序中要指定用到哪些数据,以及这些数据的类型和数据的组织形式。这就是数据结构(data structure) 。
要求计算机进行操作的步骤,也就是算法(algorithm)。
数据是操作的对象,操作的目的是对数据进行加工处理,以得到期望的结果。
著名计算机科学家沃思(Nikiklaus Wirth)提出一个公式: 算法+数据结构=程序
直到今天,这个公式对于过程化程序来说依然是适用的。
实际上,一个过程化的程序除了以上两个主要要素之外,还应当采用结构化程序设计方法进行程序设计,并且用某一种计算机语言表示。因此,算法、数据结构、程序设计方法和语言工具4个方面是一个程序设计人员所应具备的知识,在设计一个程序时要综合运用这几方面的知识。
<hr/>2.2:什么是算法
从事各种工作和活动,都必须事先想好进行的步骤,然后按部就班地进行,才能避免产生错乱。广义地说,为解决一个问题而采取的方法和步骤,就称为“算法”。
对同一个问题,可以有不同的解题方法和步骤。当然,方法有优劣之分。有的方法只须进行很少的步骤,而有些方法则需要较多的步骤。一般来说,希望采用方法简单、运算步骤少的方法。因此,为了有效地进行解题,不仅需要保证算法正确,还要考虑算法的质量,选择合适的算法。
计算机算法可分为两大类别:数值运算算法和非数值运算算法。
数值运算的目的是求数值解,例如求方程的根、求一个函数的定积分等,都属于数值运算范围。非数值运算涉及的面十分广泛,最常见的是用于事务管理领域,例如对一批职工按姓名排序、图书检索、人事管理和行车调度管理等。目前,计算机在非数值运算方面的应用远远超过了在数值运算方面的应用。
由于数值运算往往有现成的模型,可以运用数值分析方法,因此对数值运算的算法的研究比较深入,算法比较成熟。对各种数值运算都有比较成熟的算法可供选用。
<hr/>2.3:怎样表示一个算法
为了表示一个算法,可以用不同的方法。常用的方法有:自然语言、传统流程图、结构化流程图和伪代码等。
2.3.1:用自然语言表示算法
自然语言就是人们日常使用的语言,可以是汉语、英语或其他语言。用自然语言表示通俗易懂,但文字冗长,容易出现歧义。自然语言表示的含义往往不大严格,要根据上下文才能判断其正确含义。
<hr/>2.3.2:用流程图表示算法
流程图是用一些图框来表示各种操作。用图形表示算法,直观形象,易于理解。
美国国家标准化协会(American National Standard Institute,ANSI)规定了一些常用的流程图符号(见图2.3),已为世界各国程序工作者普遍采用。
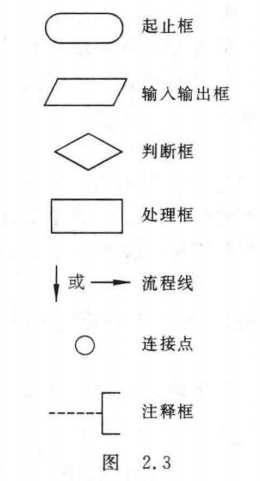
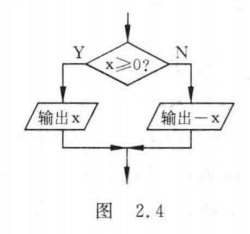
图2.3中菱形框的作用是对一个给定的条件进行判断,根据给定的条件是否成立决定如何执行其后的操作。它有一个入口,两个出口,见图2.4。
连接点(小圆圈)是用于将画在不同地方的流程线连接起来。
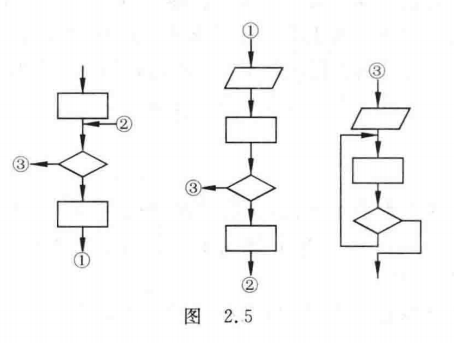
如图2.5中有两个以①为标志的连接点,它表示这两个点是连接在一起的,实际上它们是同一个点,只是画不下才分开来画。用连接点可以避免流程线交叉或过长,使流程图清晰。注释框不是流程图中必要的部分,不反映流程和操作,只是为了对流程图中某些框的操作作必要的补充说明,以帮助阅读流程图的人更好地理解流程图的作用。
——例2.1
将求1×2×3×4×5算法用流程图表示。
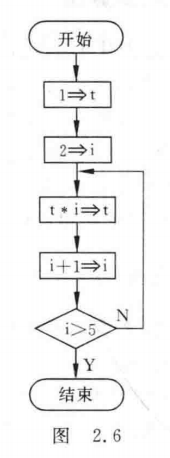
<hr/>——例2.2
有50个学生,要求输出成绩在80分以上的学生的学号和成绩。
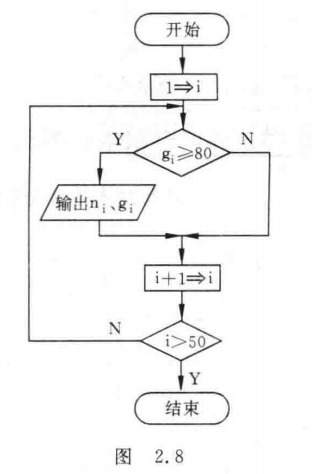
需要提醒的是:流程线不要忘记画箭头,因为它是反映流程的先后的,如不画出箭头就难以判定各框的执行次序了。
用流程图表示算法直观形象,比较清楚地显示出各个框之间的逻辑关系。有一段时期国内外计算机书刊都广泛使用这种流程图表示算法。但是,这种流程图占用篇幅较多,尤其当算法比较复杂时,画流程图既费时又不方便。在结构化程序设计方法推广之后,许多书刊已用N-S结构化流程图代替这种传统的流程图,但是每一个程序编制人员都 应当熟练掌握传统流程图,会看会画。
<hr/>2.3.3:三种基本结构
1966年,Bohra和Jacopini提出了以下3种基本结构,用这3种基本结构作为表示一个良好算法的基本单元。
如图2.14所示,虚线框内是一个顺序结构。
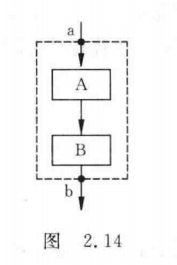
其中A和B两个框是顺序执行的。即:在执行完A框所指定的操作后,必然接着执行B框所指定的操作。顺序结构是最简单的一种基本结构。
选择结构又称选取结构或分支结构,如图2.15所示。
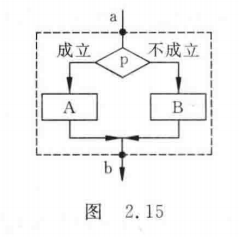
虚线框内是一个选择结构。此结构中必包含一个判断框。根据给定的条件p是否成立而选择执行A框或B框。
注意:无论p条件是否成立,只能执行A框或B框之一,不可能既执行A框又执行B框。无论走哪一条路径,在执行完A或B之后,都经过b点,然后脱离本选择结构。A或B两个框中可以有一个是空的,即不执行任何操作,如图2.16所示。
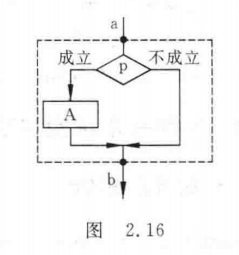
<hr/>①当型(while型)循环结构
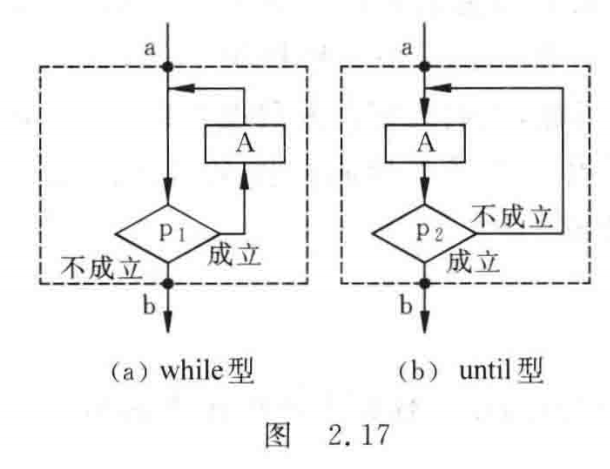
当型循环结构如图2.17(a)所示。它的作用是:当给定的条件 P_{1} 成立时,执行A框操作,执行完A后,再判断条件 P_{1} 是否成立,如果仍然成立,再执行A框,如此反复执行A框,直到某一次 P_{1} 条件不成立为止,此时不执行A框,而从b点脱离循环结构。
②直到型(until型)循环结构
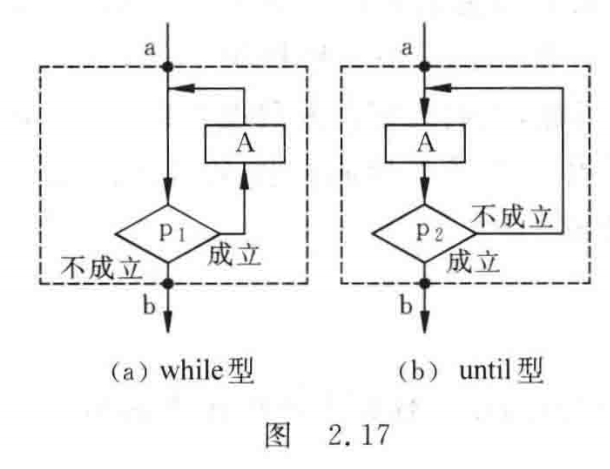
直到型循环结构如图2.17(b)所示。它的作用是:先执行A框,然后判断给定的 P_{2} 条件是否成立,如果 P_{2} 条件不成立,则再执行A,然后再对 P_{2} 条件作判断,如果 P_{2} 条件仍然不成立,又执行A……如此反复执行A,直到给定的 P_{2} 条件成立为止,此时不再执行A,从b点脱离本循环结构。
由以上3种基本结构顺序组成的算法结构,可以解决任何复杂的问题。
<hr/>2.3.4:用N-S流程图表示算法
既然用基本结构的顺序组合可以表示任何复杂的算法结构,那么,基本结构之间的流程线就是多余的了。
在N-S结构化流程图中,完全去掉了带箭头的流程线。全部算法写在一个矩形框内,在该框内还可以包含其他从属于它的框,或者说,由一些基本的框组成一个大的框。这种流程图适于结构化程序设计,因而很受欢迎。
N-S流程图用以下的流程图符号。
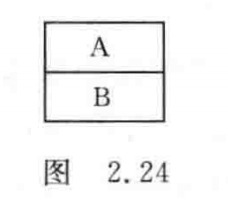
顺序结构用图2.24形式表示。A和B两个框组成一个顺序结构。
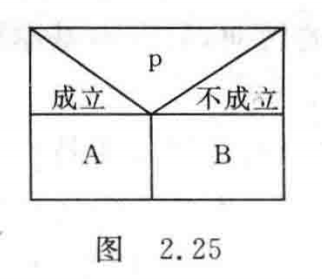
选择结构用图2.25表示。当p条件成立时执行A操作,p不成立则执行B操作。
注意:图2.25是一个整体,代表一个 基本结构。
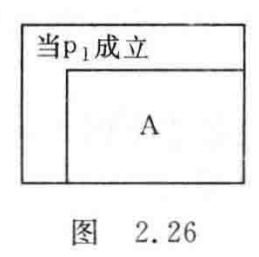
当型循环结构用图2.26形式表示,当 P_{1} 条件成立时反复执行A操作,直到 P_{1} 条件不成立为止。
直到型循环结构用图2.27形式表示。
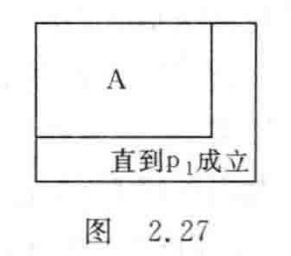
在初学时,为清楚起见,可如图2.26和图2.27那样,写明“当 P_{1} 成立”或“直到 P_{1} 成立”,待熟练之后,可以不写“当”和“直到”字样,只写“ P_{1} ”。从图的形状即可知道是当型还是直到型。
用以上3种N-S流程图中的基本框可以组成复杂的N-S流程图,以表示算法。
应当说明,在图2.24~图2.27中的A框或B框,可以是一个简单的操作(如读入数据或打印输出等),也可以是3种基本结构之一。例如,图2.24所示的顺序结构,其中的A框可以又是一个选择结构,B框可以又是一个循环结构。
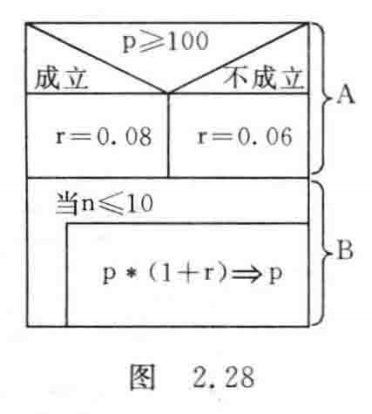
如图2.28所示那样,由A和B这两个基本结构组成一个顺序结构。
<hr/>综上所述,N-S图有以下几个优点:
(1)比文字描述更加直观形象,易于理解;
(2)没有流程线,比传统的流程图更紧凑;
(3)N-S流程图的上下顺序就是执行顺序,整个算法结构也是由各基本结构按顺序组成的。
<hr/>2.3.5:用伪代码表示算法
用传统的流程图和N-S图表示算法直观易懂,但画起来比较费事,在设计一个算法时,可能要反复修改,而修改流程图是比较麻烦的。因此,流程图适于表示一个算法,但在设计算法过程中使用不是很理想(尤其是当算法比较复杂、需要反复修改时)。为了设计算法时方便,常用一种称为伪代码(pseudo code)的工具。
伪代码是用介于自然语言和计算机语言之间的文字和符号来描述算法。用伪代码写算法并无固定的、严格的语法规则,可以用英文,也可以中英文混用。只要把意思表达清楚,便于书写和阅读即可,书写的格式要写成清晰易读的形式。
——例2.3
求5!,用伪代码表示的算法如下:

从以上例子可以看到:伪代码书写格式比较自由,容易表达出设计者的思想。同时,用伪代码写的算法很容易修改,例如加一行或删一行,或将后面某一部分调到前面某一位置,都是很容易做到的。而这却是用流程图表示算法时所不便处理的。
<hr/>2.3.6:用计算机语言表示算法
要完成一项工作,包括设计算法和实现算法两个部分。
到目前为止,只讲述了描述算法,即用不同的方法来表示操作的步骤。我们考虑的是用计算机解题,也就是要用计算机实现算法,而计算机是无法识别流程图和伪代码的,只有用计算机语言编写的程序才能被计算机执行,因此在用流程图或伪代码描述一个算法后,还要将它转换成计算机语言程序。
用计算机语言表示算法必须严格遵循所用的语言的语法规则,这是和伪代码不同的。下面将前面介绍过的算法用C语言表示。
——例2.4
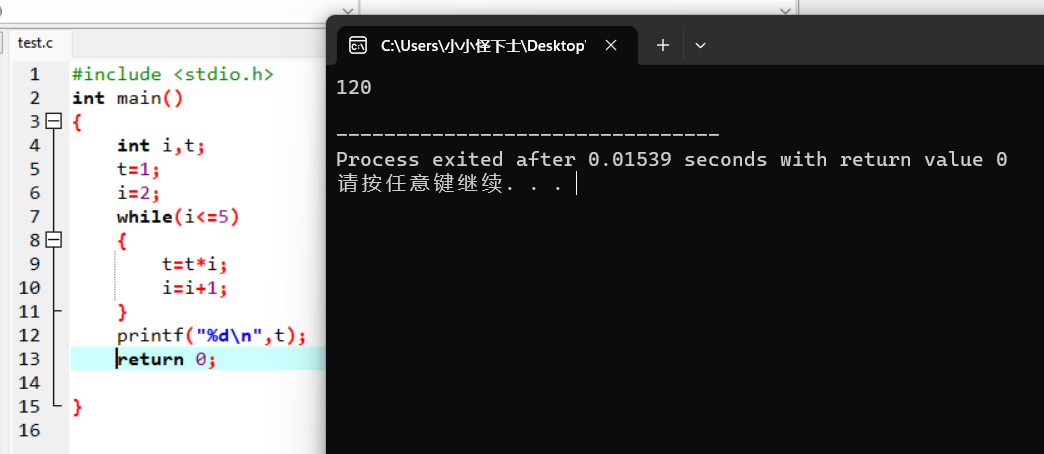
求5!,用C语言表示的算法如下: #include <stdio.h>
int main()
{
int i,t;
t=1;
i=2;
while(i<=5)
{
t=t*i;
i=i+1;
}
printf(&#34;%d\n&#34;,t);
return 0;
}
<hr/>总目录 |
|